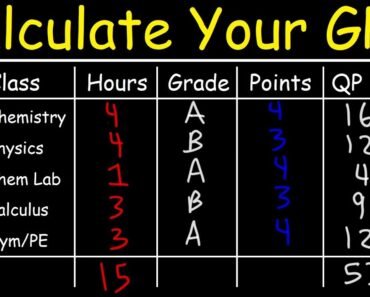
Finding the standard deviation involves several steps. It’s a measure of the amount of variation or dispersion in a set of values. Here’s how you can calculate it:
Step 1: Calculate the Mean (Average)
- Add up all the values in the dataset.
- Divide the sum by the total number of values to find the mean.
Example:
Let’s say you have the dataset: 10, 15, 20, 25, 30
- Sum = 10 + 15 + 20 + 25 + 30 = 100
- Mean = 100 / 5 = 20
Step 2: Find the Differences from the Mean
- For each value in the dataset, subtract the mean and square the result.
Example:
- For 10: (10 – 20)^2 = 100
- For 15: (15 – 20)^2 = 25
- For 20: (20 – 20)^2 = 0
- For 25: (25 – 20)^2 = 25
- For 30: (30 – 20)^2 = 100
Step 3: Find the Variance
- Add up all the squared differences from step 2.
- Divide by the total number of values minus 1 (this is called the “degrees of freedom”).
Example:
- Variance = (100 + 25 + 0 + 25 + 100) / (5 – 1) = 250 / 4 = 62.5
Step 4: Find the Standard Deviation
- Take the square root of the variance to get the standard deviation.
Example:
- Standard Deviation = √(62.5) ≈ 7.91
Note:
- The standard deviation provides a measure of how spread out the values in a dataset are around the mean. A higher standard deviation indicates greater variability.
- If you’re using a calculator or a spreadsheet program, there are built-in functions to calculate standard deviation. These tools can make the process faster and more accurate.
Remember, standard deviation is a powerful tool for understanding the variability within a dataset, and it’s widely used in statistics and data analysis.